[자료구조] - 그래프 (Graph)

---

---

그래프 개요

오늘 다룰 그래프 자료구조의 대표적이 예시로는 지하철 노선도가 있습니다. 역들이 연결된 지하철 노선도를 그래프로 표현하면 특정 역에서 또 다른 역으로 가는 최단 경로를 계산할 수 있게 됩니다. 선형 리스트나 트리로는 표현하기 어려운 문제들을 그래프를 통하여 쉽게 해결할 수 있습니다. 지금부터 그래프 자료구조에 대해서 알아보도록 하겠습니다.

---

그래프의 정의와 용어

출처: https://i.imgur.com/SYsNnEB.png

그래프는 객체 사이의 연결 관계를 표현할 수 있는 자료구조입니다. 그래프는 정점(Vertex)과 간선(Edge)의 집합입니다. 수학적으로는 $G = (V, E)$로 나타낼 수 있습니다. $V(G)$는 그래프 G의 정점들의 집합을 나타내며, $E(G)$는 그래프 G의 간선들의 집합을 나타냅니다.

지금부터 그래프 자료구조 를 이해하기 위하여 반드시 필요한 용어들을 알아보겠습니다.

• 정점(Vertex): 여러 가지 특성을 가질 수 있는 객체, 노드라고도 불린다.
• 간선(Edge): 정점 사이의 관계, 링크라고도 불린다.
• 인접 정점: 간선에 의해 직접 연결된 정점
• 차수: 특정 정점에 인점한 정점의 수
• 경로: 정점 s로부터 정점 n까지 간선으로 연결된 정점을 순서대로 나열한 리스트
• 단순 경로: 경로 중 반복되는 간선이 없는 경로
• 사이클: 단순 경로의 시작 정점과 종료 정점이 동일한 경로

---

그래프의 종류

그래프의 종류는 다양합니다. 무방향 그래프, 방향 그래프, 가중치 그래프, 부분 그래프, 연결 그래프, 완전 그래프 하나하나 살펴보도록 하겠습니다.

무방향 그래프와 방향 그래프

간선의 종류에 따라 그래프는 무방향 그래프와 방향 그래프로 나뉩니다.
무방향 그래프는 간선을 통해 양방향으로 이동할 수 있으며 정점 A와 정점 B를 연결하는 간선은 (A, B)로 표현되고 (A, B)와 (B, A)는 동일합니다.

방향 그래프는 간선을 통해 한 방향으로만 이동할 수 있으며 정점 A와 정점 B를 연결하는 간선은 <A, B>로 표현되고 <A, B>와 <B, A>는 서로 다릅니다.

가중치 그래프 (네트워크)

간선에 가중치를 할당하여, 단순히 두 정점간의 연결 관계를 넘어 연결 강도까지 나타낼 수 있도록 한 그래프를 가중치 그래프라고 합니다. 또한 네트워크라고 불리기도 합니다. 가중치 그래프는 간선의 가중치로 인하여 더욱 복잡한 관계를 표현할 수 있습니다.

부분 그래프

어떤 그래프의 정점과 간선의 일부로 이루어진 그래프를 부분 그래프라고 합니다. 즉, 어떤 그래프의 부분집합인 그래프입니다. 그렇기에 그래프 G의 부분 그래프의 그래프 S는 다음 수식을 만족시킵니다.

$$ V(S) \subseteq V(G) $$

$$ E(S) \subseteq E(G) $$

연결 그래프와 비연결 그래프

무방향 그래프 G에 있는 모든 정점쌍에 대해 항상 경로가 존재하면 G는 연결되었다고 하고, 이때 G는 연결 그래프라고 부릅니다. 반면, 그렇지 않은 그래프는 비연결 그래프(단절 그래프)라고 합니다.

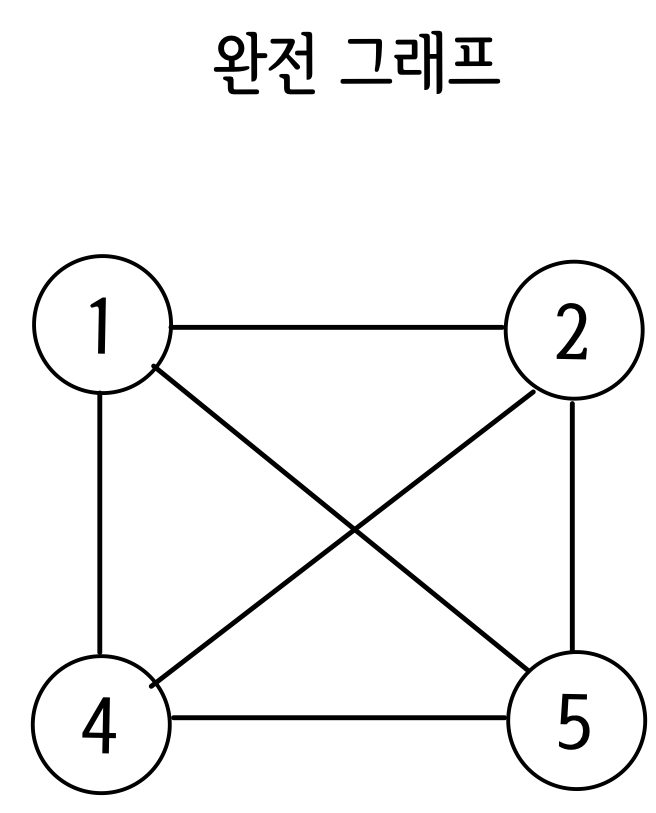
완전 그래프

그래프에 있는 모든 정점이 서로 연결되어 있는 그래프는 완전 그래프라고 합니다. 완전 그래프의 정점 수가 n이라면, 간선의 수는 $n \times (n - 1) /2$가 됩니다.

---

그래프 표현 방법

그래프 자료구조를 표현하는 방법에는 2가지 방법이 있습니다. 바로 "인접 행렬" 표현 방법과 "인접 리스트" 표현 방법입니다. 이 두 가지 방법은 각각 메모리 사용량, 처리 시간 등이 다르기에 문제 상황에 적절한 표현 방법을 선택해야 합니다.

• 인접 행렬(Adjacency Matrix): 2차원 배열을 사용하여 그래프를 표현한다. n개의 정점을 가지는 그래프를 인접 행렬로 표현하기 위해서는 항상 $n^2$개의 메모리 공간이 필요하다. 그렇기에 간선이 많이 존재하는 그래프를 표현할 때는 적합하지만, 간선이 적은 경우는 적합하지 않다. 또한 두 정점을 연결하는 간선의 존재 여부를 $O(1)$ 시간 안에 즉시 알 수 있으나, 그래프에 존재하는 모든 간선의 수를 알아내려면 $O(n^2)$ 시간이 요구된다.
• 인접 리스트(Adjacency List): 연결 리스트를 사용하여 그래프를 표현한다. 정점의 수가 n개이고 간선이 e개인 무방향 그래프를 표현하기 위해서는 n개의 연결 리스트가 필요하고 n개의 헤더 노드와 2e개의 노드가 필요하다. 그렇기에 인접 리스트 표현은 간선의 개수가 적은 희소 그래프를 표현하기에 적합하다. 또한 그래프에 존재하는 모든 간선의 수를 알아내려면 $O(n+e)$ 시간이 요구된다.

그래프 구현

그래프 자료구조를 C언어에서 구현하는 방법은 다음과 같습니다. 인접 행렬로 구현하는 그래프와 인접 리스트로 구현하는 그래프를 나누어서 살펴보겠습니다.

인접 행렬로 구현한 그래프

#include <stdio.h>
#include <stdlib.h>

#define MAX_VERTICES 50 
typedef struct GraphType {
    int n; // 정점의 개수
    int adj_mat[MAX_VERTICES][MAX_VERTICES];
} GraphType;

// 그래프 초기화
void init(GraphType* g) {
    int r, c;
    g->n = 0;
    for (r = 0; r<MAX_VERTICES; r++) 
        for (c = 0; c<MAX_VERTICES; c++)
            g->adj_mat[r][c] = 0;
}

// 정점 삽입 연산
void insert_vertex(GraphType* g, int v) {
    if (((g->n) + 1) > MAX_VERTICES) {
        fprintf(stderr, "그래프: 정점의 개수 초과");
        return;
    }
    g->n++;
}

// 간선 삽입 연산
void insert_edge(GraphType* g, int start, int end) {
    if (start >= g->n || end >= g->n) {
        fprintf(stderr, "그래프: 정점 번호 오류");
        return;
    }
    g->adj_mat[start][end] = 1;
    g->adj_mat[end][start] = 1;
}

// 인접 행렬 출력 함수
void print_adj_mat(GraphType* g) {
    for (int i = 0; i < g->n; i++) {
        for (int j = 0; j < g->n; j++) {
            printf("%2d ", g->adj_mat[i][j]);
        }
        printf("\n");
    }
}

int main() {
    GraphType *g;
    g = (GraphType *)malloc(sizeof(GraphType));
    init(g);
    for (int i = 0; i < 4; i++) 
        insert_vertex(g, i);
    insert_edge(g, 0, 1);
    insert_edge(g, 0, 2);
    insert_edge(g, 0, 3);
    insert_edge(g, 1, 2);
    insert_edge(g, 2, 3);
    print_adj_mat(g);

    free(g);

    return 0;
}

인접 리스트로 구현한 그래프

#include <stdio.h>
#include <stdlib.h>

#define MAX_VERTICES 50
typedef struct GraphNode {
    int vertex;
    struct GraphNode* link;
} GraphNode;

typedef struct GraphType {
    int n; // 정점의 개수
    GraphNode* adj_list[MAX_VERTICES];
} GraphType;

// 그래프 초기화
void init(GraphType* g) {
    int v;
    g->n = 0;
    for (v = 0; v < MAX_VERTICES; v++) 
        g->adj_list[v] = NULL;
}

// 정점 삽입 연산
void insert_vertex(GraphType* g, int v) {
    if (((g->n) + 1) > MAX_VERTICES) {
        fprintf(stderr, "그래프: 정점의 개수 초과");
        return;
    }
    g->n++;
}

// 간선 삽입 연산, v를 u의 인접 리스트에 삽입한다.
void insert_edge(GraphType* g, int u, int v) {
    GraphNode* node;
    if (u >= g->n || v >= g->n) {
        fprintf(stderr, "그래프: 정점 번호 오류");
        return;
    }
    node = (GraphNode *)malloc(sizeof(GraphNode));
    node->vertex = v;
    node->link = g->adj_list[u];
    g->adj_list[u] = node;
}

// 인접 리스트 출력 함수
void print_adj_list(GraphType* g) {
    for (int i = 0; i < g->n; i++) {
        GraphNode* p = g->adj_list[i];
        printf("정점 %d의 인접 리스트 ", i);
        while (p != NULL) {
            printf("-> %d ", p->vertex);
            p = p->link;
        }
        printf("\n");
    }
}

int main() {
    GraphType *g;
    g = (GraphType *)malloc(sizeof(GraphType));
    init(g);
    for (int i = 0; i < 4; i++) 
        insert_vertex(g, i);
    insert_edge(g, 0, 1);
    insert_edge(g, 1, 0);
    insert_edge(g, 0, 2);
    insert_edge(g, 2, 0);
    insert_edge(g, 0, 3);
    insert_edge(g, 3, 0);
    insert_edge(g, 1, 2);
    insert_edge(g, 2, 1);
    insert_edge(g, 2, 3);
    insert_edge(g, 3, 2);
    print_adj_list(g);
    free(g);

    return 0;
}

---