01. 진법 체계

진법은 사용할 수 있는 숫자의 개수와 각 숫자의 위치 값을 정의한 수의 체계이다.
이때, 사용할 수 있는 숫자의 개수는 "0부터 해당 진법의 수보다 1 적은 수'이다.
우리가 주로 사용하는 진법은 10진법이지만 2진법, 8진법, 16진법, 60진법 등 많은 진법이 사용되고 있다.
그 중 컴퓨터는 2진법을 사용한다. 컴퓨터가 표현하는 체계를 이해하기 위해 다양한 진법들에 대해서 알아보자.
1) 10진법(Decimal Notation)
10진법: 0부터 9까지 10개의 숫자를 한 묶음으로 해서 1자리씩 위로 올리는 방법
| $$ \begin{align} 432_{10} &= 4 \times 10^2 + 3 \times 10^1 + 2 \times 10^0 \\&= 4 \times 100 + 3 \times 10 + 2 \\&= 432 \end{align} $$ |
2) 2진법(Binary Notation)
2진법: 0과 1이라는 두 개의 숫자만으로 수를 나타내는 진법
다만 0과 1만으로 수를 표현하기에 숫자가 커지면 숫자열이 굉장히 길어지게 된다.
이러한 가독성이 좋지 않다는 단점을 보완하기 위해 8진법과 16진법으로 바꿔서 표현하기도 한다.
| $$ \begin{align} 1101_{2} &= 1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 \\&= 1 \times 8 + 1 \times 4 + 0 \times 2 + 1 \times 1 \\&= 8 + 4 + 0 + 1 \\&= 13 \end{align} $$ |
3) 8진법(Octal notation)
8진법: 0부터 7까지 8개의 숫자로 수를 표현하는 방법
2진수를 3자리씩 묶어서 빠르게 표현 가능하다.
| $$ \begin{align} 257_{8} &= 2 \times 8^2 + 5 \times 8^1 + 7 \times 8^0 \\&= 2 \times 64 + 5 \times 8 +7 \times 1 \\&= 128 + 40 + 7 \\&= 175 \end{align} $$ |
4) 16진법(Hexadecimal Notation)
16진법: 0~9까지의 숫자와 A~F까지의 문자를 함께 사용하여 수를 표현하는 방법
4비트로 1자리의 수를 표현하는 방법이기에 컴퓨터에서 널리 쓰인다.
| $$ \begin{align} 2AD_{16} &= 2 \times 16^2 + A \times 16^1 + D \times 16^0 \\&= 2 \times 256 + 10 \times 16 + 13 \times 1 \\&= 512 + 160 + 13 \\&= 685 \end{align} $$ |
02. 진법 변환
1) 10진수 -> N진수 변환 (정수일 때)
1. 10진수를 변환하고자 하는 진법의 기수(2진법이면 2, 8진법이면 8, 16진법이면 16)로 나누고, 기록한다.
2. 나눈 몫을 다시 변환하고자 하는 진법의 기수로 나누고, 해당 나머지를 기록한다.
3. 계속 이 방법으로 나누고 더 이상 나눌 수 없을 때 끝을 낸다.
4. 마지막 몫과 기록한 나머지들을 순서대로 적으면 해당 진법의 수가 나오게 된다.
Ex) 10진수 41은 2진수로 변환하면 101001이 나오게 된다!!

2) 10진수 -> 2진수 변환 (소수가 있을 때)
(0. 소수점이 있을 때 정수가 0이면 바로 계산하고, 정수가 0이 아니면 정수와 소수부분을 분리하여 계산한다.)
Ex) "0.6875" 라면 바로 밑의 과정 진행, "35.6875" 라면 "35 + 0.6875" 로 정수와 소수를 따로 계산을 진행한다.
1. 소수점이 있는 경우에는 소수점 아래의 소수 부분에 2를 계속 곱하면서 정수로 자리 올림이 발생하는지 확인한다.
2. 이때 자리올림이 발생하는 경우 1이 소수점 자리에 위치하게 되고 자리올림이 발생하지 않는 경우에는 0이 소수점 자리에 위치하게 된다.
3. 이 과정을 계속 진행하여 소수점 아래 부분이 모두 "0"이 되는 경우 계산이 종료된다.
Ex) 0.6875 X 2 = 1.3750이 되는데 이때 올라간 정수 "1"은 2진수에서 0.1이 된다. 그리고 소수 부분만 다시 분리하여 0.3750을 만들고 다시 X 2를 진행한다. 이때는 0.7500이 되기 때문에 정수 "0"이 그 다음 소수점 자리에 위치하여 0.10이 된다.

3) 2진수 -> 10진수 변환 (정수일 때)
1. 2진수의 0과 1을 각 자릿수만큼의 2의 지수 제곱으로 곱한다.
2. 각자 곱한 값들을 모두 더하면 계산은 끝이 난다.
| $$ \begin{align} 101001_{2} &= 1 \times 2^5 + 1 \times 2^3 + 1 \times 2^0 \\&= 1 \times 32 + 1 \times 8 + 1 \times 1 \\&= 32 + 8 + 1 \\&= 41_{10} \end{align} $$ |
4) 2진수 -> 10진수 변환 (소수가 있을 때)
1. 정수의 변환 방식과 동일하게 각 자릿수를 고려해 계산한다.
2. 다만, 소수점 아래로 내려갈수록 지수 제곱이 커지고 마이너스를 붙여 계산한다.
(소수점 아래로 내려갈수록 지수 제곱 자체는 작아진다는 뜻이다. -1, -2, -3, -4 ...)
| $$ \begin{align} 0.1011_{2} &= 1 \times 2^{-1} + 0 \times 2^{-2} + 1 \times 2^{-3} + 1 \times 2^{-4} \\&= 1 \times 0.5 + 1 \times 0.125 + 1 \times {0.0625} \\&= 0.5 + 0.125 + 0.0625 \\&= 0.6875_{10} \end{align} $$ |
03. 데이터 표현
01) 정수 표현
정수는 양의 정수(자연수), 0, 음의 정수(-1, -2, -3...)으로 구성되어 있다.
컴퓨터에서 정수는 부호 있는 정수와 부호 없는 정수로 나뉜다.
(1) 부호 없는 정수
말 그대로 부호를 생략한다는 의미로, 모든 숫자는 0 또는 양의 정수로 표현된다.
8비트로 부호 없는 정수를 표현하면 $0_{10} ~ 255_{10}(= 2^8 - 1)$ 표현이 가능하다.
즉, n비트를 사용한 부호 없는 정수 표현은 0부터 $(2^n -1)$ 까지이다.
| $$ 0000 \, 0000_2 \leftrightarrow 0_{10} \\ 1111 \, 1111_2 \leftrightarrow 255_{10} $$ |
(2) 부호 있는 정수
부호 있는 정수는 음수의 표현까지 고려한다.
이러한 부호 있는 정수 표현에는 "부호화 절댓값 표현"과 "보수 표현"이 있다.
"부호화 절댓값 표현"은 가장 왼쪽에 위치한 비트인 "최대유효비트"가 0이면 양의 정수(이때 0 포함)로, "최대유효비트가 1이면 음의 정수(-0 포함)로 표현되는 방식이다.
8비트를 이용하여 부호화 절댓값을 표현할 떄는 절댓값 계산을 위해 7비트까지만 사용할 수 있다.
즉, n비트를 사용한 부호 없는 정수 표현은 $-(2^{n-1} -1)$부터 $+(2^{n-1} -1)$ 까지이다.
| $$ 0000 \, 0101_2 \rightarrow +5_{10} \\ 1000 \, 0101_2 \rightarrow -5_{10} $$ |
02) 보수 표현
보수 표현은 부호화 절대값의 단점을 해결한 부호 있는 정수 표현 방법이다.
-부호화 절댓값 표현의 단점-
"부호 결정에 1비트를 써서 표현하는 수의 범위가 줄어든다."
"+0과 -0이라는 0에 대한 두 가지 표현이 존재한다."
보수는 "두 수의 합이 진수의 밑수(N)가 되게 하는 수"를 말한다.
예를 들어 "10진수 2"의 10의 보수는 "10진수 8"이고, "10진수 6"의 10의 보수는 "10진수 4"이다.
n진법으로 표시된 정수를 기준으로 n-1의 보수 표현법과 n의 보수 표현법이 존재한다.
대표적으로 컴퓨터가 사용하는 2진법에는 1의 보수와 2의 보수가 있는데 이에 대해서 알아보자.
(1) 1의 보수 표현
1의 보수는 "어떤 2진수의 비트를 반전"시켜서 얻을 수 있다.
즉, 0 -> 1, 1 -> 0로 바꾸는 것이다.
Ex) 2진수 1010의 1의 보수는 0101이다.
(2) 2의 보수 표현
2의 보수는 "어떤 2진수의 비트를 반전시킨 후 결과값에 1을 더해서" 얻을 수 있다.
즉, 어떤 2진수를 1의 보수로 바꾼 후 제일 뒤에 1을 더해주는것과 같다.
컴퓨터는 기본적으로 2의 보수 표현을 사용한다.
Ex) 2진수 1010의 2의 보수는 0110이다.
(3) 보수 표현 사칙 연산
덧셈: 2진수에서 덧셈은 10진수에서 덧셈과 계산 방식이 동일하다.
Ex) 2진수 0101 + 2진수 0110 = 2진수 1011
뺄셈: 2진수에서는 뺄셈 계산이 불가능하기에 보수를 이용하여 계산한다.
1의 보수 뺄셈
가장 먼저 빼는 수의 1의 보수를 구한 후 더한다.
그 후, 덧셈결과에 자리올림이 생기면 최하위 비트에 1을 더한후 자리올림 된 수를 제거한다.
그 후, 덧셈결과에 자리올림이 생기지 않으면 "연산 결과"의 1의 보수를 구한 후 '-' 부호를 붙인다.
Ex) 2진수 1101 - 2진수 1001
=> 1101 + (1001의 1의 보수)
=> 1101 + 0110 = 10011
=> (최하위 비트에 1 더함 = 10100)
=> (자리올림 수 제거 = 0100)
=> 답은 0100이다.
Ex) 2진수 0101 - 2진수 0110
=> 0101 + (0110의 1의 보수)
=> 0101 + 1010 = 1111
=> (1111의 1의 보수 = 0)
=> (부호 붙여서 -0)
답은 -0이다.
2의 보수 뺄셈
가장 먼저 빼는 수의 2의 보수를 구한 후 더한다.
그 후, 덧셈결과에 자리올림이 생기면 자리올림이 생긴 수를 제거한다, 그리고 그 값이 결과이다.
그 후, 덧셈결과에 자리올림이 생기지 않으면 "연산 결과"의 2의 보수를 구한 후 '-' 부호를 붙인다.
Ex) 2진수 1101 - 2진수 1001
=> 1101 + (1001의 2의 보수)
=> 1101 + 0111 = 10100
=> (자리올림 수 제거 = 0100)
=> 답은 0100이다.
Ex) 2진수 0101 - 2진수 1001
=> 0101 + (1001의 2의 보수)
=> 0101 + 0111 = 1100
=> (1100의 2의 보수 = 0100)
=> (부호 붙여서 -0100)
답은 -0100이다.
03) 실수 표현
실수는 유리수와 무리수를 총칭하여 확장한 수이다.
즉, 수직선 위에 나타낼 수 있는 모든 수를 뜻한다.
컴퓨터 내에서 실수를 표현하는 방법으로는 "고정소수점 표현"과 "부동소수점 표현"이 있다.
(1) 고정소수점 표현
고정소수점 표현은 말 그대로 소수점의 위치를 고정시켜 표현한다는 의미이다.
16비트를 사용하는 경우, 앞의 8비트는 정수 부분과 부호 부분을 표현하고, 나머지 8비트는 소수 부분을 표현한다.
즉, 소수점의 위치를 고정시켜서 정수를 표현하는 부분과 소수를 표현하는 부분을 나눈다는 것이다.
Ex) $5.34_{10} = 101. 01010111_2$
이때, 정수부의 경우 뒷자리부터 채우며, 소수부의 경우 앞자리부터 채운다.
그리고 남는 부분은 모두 0으로 채운다.
=> 00000101.01010111
고정소수점 표현은 숫자표현이 간단하기 때문에 구현하기가 편하고 연산 속도가 빠르지만 표현 가능한 수가 적고 제한된 부분에서만 사용한다. 그래서 컴퓨터에서는 이 방식을 사용하지 않는다.
(2) 부동소수점 표현
부동소수점 표현은 소수점의 위치를 고정시키지 않고 가수와 지수를 사용해 실수를 표현한다는 의미이다.
여기서 가수는 유효숫자를 나타내며, 지수는 소수점의 위치를 나타내고, 부호는 가수의 부호를 나타낸다
10진수 $0.34_{10}$을 2진수로 바꾸면 $0.010101110_2$이 되는데 이를 부동소수점 표현으로 나타내려면
먼저 "정규형"으로 바꿔야 한다. 정규형은 정수 부분에 "0이 아닌 수를 하나만 남기는 것"이다.
즉, 정규형은 2진수를 1.xxxxxxx $\times 2^n$로 나타내는 것을 말한다.
$0.010101110_2$ 을 정규형으로 표현하면 $1.0101110 \times 2^{-2}$이 되는데,
이제 정규형 표현에서 지수와 가수를 나누면 된다.
8비트에서는 부호 1비트, 지수 3비트, 가수 4비트를 할당한다.
16비트의 경우 부호 1비트 지수 5비트, 가수 10비트로 구성된다.
32비트의 경우 부호 1비트 지수 8비트, 가수 23비트로 구성된다.
64비트의 경우 부호 1비트 지수 11비트, 가수 52비트로 구성된다.
8비트로 할당하기 때문에 지수에는 3비트를 할당한다.
이때, 음수 형태의 지수를 표현하기 위해 "초과표현"을 사용한다.
초과표현은 $2^{n-1} - 1$ (n : 지수 bit) 방식으로 구할 수 있다.
$1.0101110 \times 2^{-2}$에서 가수의 부호는 +이기에 부호할당에 0을 적는다.
$1.0101110 \times 2^{-2}$ 에서 지수에 3비트를 할당하기에 3초과표현을 사용한다.
이때 지수가 -2이기 때문에 3을 초과시켜 지수 부호할당에 1을 적는다. (정확히는 001)
그리고 가수에서 4비트만 사용하기에 앞에서 4비트를 잘라 1010을 적는다.
결론적으로 $0.34_{10}$는 컴퓨터 내부에서 $0 \, 001 \, 1010 \rightarrow 00011010_{2}$로 저장된다.
04) 문자 표현
컴퓨터는 기본적으로 숫자만 다루지만 인간은 문자로 소통한다.
이로 인해, 컴퓨터로도 문자를 처리하기 위해 숫자와 문자를 대응하는 코드를 사용하는데,
대표적으로 '아스키코드'와 '유니코드'가 있다.
(1) 아스키코드
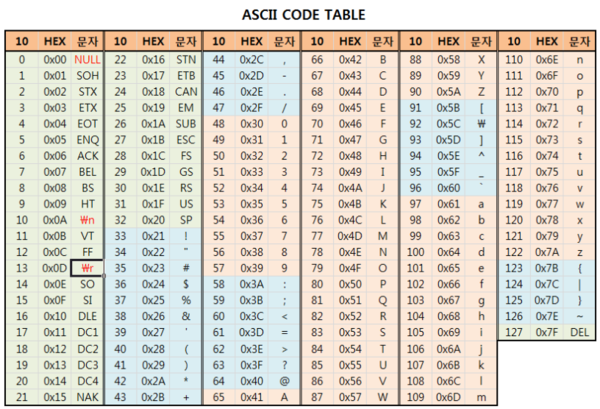
아스키코드는 미국 표준 협회에서 만든 코드이며, 7비트로 구성되어 있다.
7비트로 구성되었기 때문에 표현할 수 있는 문자 수는 128$(=2^7)$ 개이다.
(2) 유니코드
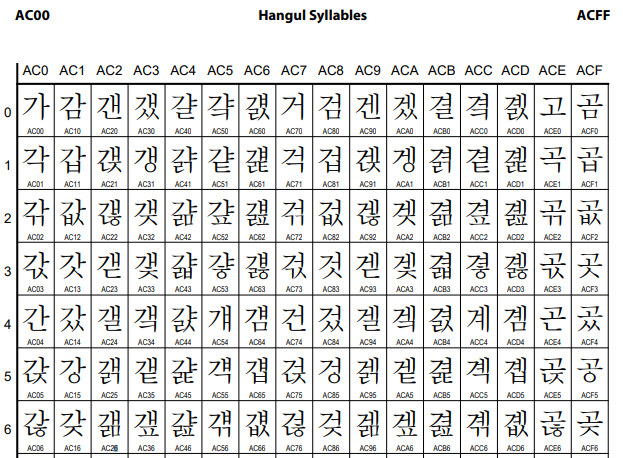
아스키코드에는 여러 나라의 언어를 모두 표현할 수 없다는 단점이 있다. 그를 보완하기 위해 유니코드가 만들어졌다.
유니코드는 언어와 상관없이 모든 문자를 16비트로 표현한다.
16비트로 구성되었기 때문에 표현할 수 있는 문자 수는 65,536$(=2^{16})$ 개이다.
