이산수학에서 다루는 행렬은 기초적인 행렬입니다. 좀 더 심화적인 행렬의 내용은 선형대수학을 포스팅할 때 다루도록 하겠습니다.

행렬의 정의
행렬은 행과 열로 나열하는 것을 말합니다. 기본적으로 연립방정식을 풀기 위하여 만들어진 개념이며, 수, 문자, 함수 등을 괄호 안에 배열한 것입니다. 행렬의 각 성분은 실수여야 하고, 이는 “스칼라(Scalar)”라고 합니다. 스칼라는 크기만 있고 방향을 가지지 않는 양을 말하며, 벡터와는 반대되는 개념입니다. 수학적으로 정의한 행렬은 다음과 같습니다.
💡 (정의) 행렬 💡
행렬 $A$는 실수들을 사각형의 배열로 표시한 것이다(단, $m$과 $n$은 양의 정수). 각각 $n$쌍으로 된 $m$개의 수평 성분 ($a_{i1} \ a_{i2} \ a_{i3} \cdots a_{in}$ ) (단, $1 \leq i \leq m$ )을 $A$의 행(row)이라고 하고, 각각 $m$쌍으로 된 $n$개의 수직 성분 ($a_{1j} \ a_{2j} \ a_{3j} \cdots a_{mj}$ )(단, $1 \leq j \leq n$)을 $A$의 열(column)이라고 한다.
$$ A = \begin{pmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} \\ && \vdots && \\ a_{m1} & a_{m2} & a_{m3} & \cdots & a_{mn}\end{pmatrix} $$
행렬 $A$를 $A = (a_{ij})$로 표시하는데, 이때, 원소 $a_{ij}$는 $i$행의 $j$번째 열의 원소를 나타냅니다. $A$를 $m \times n$ 행렬이라고 하며, $m \ by \ n$ 행렬로 읽습니다.
영행렬
만약 각 성분이 모두 0이라면, 이 행렬을 “영행렬”이라고 하고 0으로 표시합니다.
💡 (정의) 영행렬 💡
각 성분이 0인 행렬을 말한다. 영행렬은 $0$으로 표시한다.
$$ \begin{pmatrix} 0 & 0 \\ 0 & 0\end{pmatrix}, \begin{pmatrix} 0 &0 & 0 \\ 0 & 0 & 0\end{pmatrix}, \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{pmatrix} $$
두 행렬의 같음
두 행렬이 있을 때, 그 두 행렬이 같을 조건은 다음과 같습니다.
💡 (정의) 두 행렬의 같음 💡
두 행령이 $m \times n$ 행렬이고 대응하는 원소가 모두 같으면 $A = (a_{ij})$와 $B = (b_{ij})$는 같다라고 하며, $A = B$ 라고 표현합니다.
행렬의 합
행렬의 합은 다음과 같이 정의합니다.
💡 (정의) 행렬의 합 💡
행렬 $A$와 $B$가 같은 크기와 행과 열을 가지면, 행렬 $A$와 $B$의 행렬의 합은 $A + B$로 표시하고 $A + B = (a_{ij}) + (b_{ij}) = (a_{ij}+b_{ij})$이다. 즉, 대응하는 성분끼리 합을 구하면 그 값이 $A + B$의 각 성분이 되는 것이다.
행렬의 덧셈 성질
행렬의 합을 통하여 알 수 있는 행렬의 덧셈 성질은 다음과 같습니다.
💡 (정리) 행렬의 덧셈 성질 💡
- $A + B = B + A$ (덧셈의 교환법칙)
- $(A + B) + C = A + (B + C)$ (덧셈의 결합법칙)
- $A + 0 = 0 + A = A$ (덧셈의 항등법칙)
행렬의 곱
행렬의 곱은 스칼라곱과 행렬곱 두 가지로 정의됩니다.
스칼라 곱
스칼라 곱은 행렬에 실수배를 하는 것입니다. 스칼라 곱은 다음과 같이 정의됩니다.
💡 (정의) 스칼라 곱 💡
$A$가 $m \times n$ 행렬이고 $c$가 실수이면 다음이 성립한다.
$$ c \cdot A = c \cdot (a_{ij}) = (c \times a_{ij}) $$
행렬의 곱
두 행렬을 곱하는 행렬의 곱은 다음과 같이 정의됩니다.
💡 (정의) 행렬의 곱 💡
$A = (a_{ij})$는 $m \times p$ 행렬이고 $B = (b_{ij})$는 $p \times n$ 행렬일 때, 행렬의 곱 $AB$는 $m \times n$ 행렬이고 $C = (c_{ij})$가 된다. 이때,
$$ C_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} \cdots + a_{ip}b_{pj} \quad (\text{단, } 1 \leq i \leq m, \ 1 \leq j \leq n) $$
이다. 즉, 행렬의 곱 $AB$는 다음과 같이 구할 수 있다.
$$ \begin{aligned}
AB &=
\begin{pmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1p} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2p} \\ && \vdots && \\ a_{i1} & a_{i2} & a_{i3} & \cdots & a_{ip} \\ && \vdots && \\ a_{m1} & a_{m2} & a_{m3} & \cdots & a_{mp}\end{pmatrix}
\begin{pmatrix} b_{11} & b_{12} & b_{13} & \cdots b_{1j} & \cdots & b_{1n} \\ b_{21} & b_{22} & b_{23} & \cdots b_{1j} & \cdots & b_{2n} \\ && \vdots && \\ && \vdots && \\ && \vdots && \\ b_{p1} & b_{p2} & b_{p3} & \cdots b_{1j} & \cdots & b_{pn}\end{pmatrix}
\\ &=
\begin{pmatrix} c_{11} & c_{12} & c_{13} & \cdots & c_{1n} \\ c_{21} & c_{22} & c_{23} & \cdots & c_{2n} \\ && \vdots && \\ & \cdots & c_{ij} & \cdots \\ && \vdots && \\ c_{m1} & c_{m2} & c_{m3} & \cdots & c_{mn}\end{pmatrix}
\end{aligned} $$
행렬의 곱셈 성질
행렬의 곱을 통하여 알 수 있는 행렬의 곱셈 성질은 다음과 같습니다.
💡 (정리) 행렬의 곱셈 성질 💡
- $A \cdot (B \cdot C) = (A \cdot B) \cdot C$ (곱셈의 결함법칙)
- $A \cdot (B + C) = A \cdot B +A \cdot C$ (곱셈의 분배법칙)
- $(A + B) \cdot C = A \cdot C + B \cdot C$ (곱셈의 분배법칙)
특수 행렬
여태껏 기본 행렬에 대해서 알아보았는데, 지금부터는 다양한 형태의, 여러 종류의 행렬들에 대해서 알아보도록 하겠습니다.
정방 행렬
💡 (정의) 정방 행렬 💡
행과 열의 수가 $n$으로 같은 행렬을 $n$차 정방 행렬이라고 한다.
이때, 행 또는 열의 개수를 “정방 행렬의 차수”라고 하며, $n$차 정방 행렬에서 대각선상에 위치한 원소, $a_{ii}(i = 1, \ 2, \ 3, \cdots, \ n)$를 “주대각 원소”라고 합니다.
대각 행렬
💡 (정의) 대각 행렬 💡
주대각 원소를 제외한 나머지 원소가 모두 $0$인 행렬을 대각 행렬이라고 한다.
$$ \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}, \ \begin{pmatrix} 2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 4 \end{pmatrix} $$
단위 행렬(= 항등 행렬)
💡 (정의) 단위 행렬(항등 행렬) 💡
주대각 원소들은 모두 $1$이고, 주대각 원소를 제외한 나머지 원소들은 모두 $0$인 정방 행렬을 단위 행렬 또는 항등 행렬이라고 한다.
$$ \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \ \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$
스칼라 행렬
💡 (정의) 스칼라 행렬 💡
주대각 원소들이 모두 같은 값을 갖는 대각 행렬을 스칼라 행렬이라고 한다.
$$ \begin{pmatrix} 3 & 0 \\ 0 & 3 \end{pmatrix}, \ \begin{pmatrix} 5 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 5 \end{pmatrix} $$
전치 행렬
💡 (정의) 전치 행렬 💡
행렬 $A$가 임의의 $m \times n$ 행렬일 때, $A$의 행과 열을 바꾼 $n \times m$ 행렬을 전치행렬이라고 한다. $A$의 전치행렬은 $A^T$라고 표현한다.
대칭 행렬
💡 (정의) 대칭 행렬 💡
어떤 정방 행렬이 자신과 자신의 전치 행렬이 같으면 그 행렬을 대칭 행렬이라고 한다. 행렬 $A$가 대칭 행렬이면 $A = A^T$를 만족한다.
삼각 행렬
상삼각 행렬이거나 하삼각 행렬을 간단하게 삼각 행렬이라고 합니다.
💡 (정의) 상삼각 행렬 💡
주대각 원소의 아래쪽에 있는 모든 원소들이 $0$인 정방 행렬을 상삼각 행렬이라고 한다.
$$ \begin{pmatrix} 3 & 5 \\ 0 & 4 \end{pmatrix}, \ \begin{pmatrix} 5 & 6 & 7 \\ 0 & 8 & 9 \\ 0 & 0 & 3 \end{pmatrix} $$
💡 (정의) 하삼각 행렬 💡
주대각 원소의 위쪽에 있는 모든 원소들이 $0$인 정방 행렬을 상삼각 행렬이라고 한다.
$$ \begin{pmatrix} 3 & 0 \\ 5 & 4 \end{pmatrix}, \ \begin{pmatrix} 5 & 0 & 0 \\ 6 & 7 & 0 \\ 8 & 9 & 3 \end{pmatrix} $$
띠 행렬
💡 (정의) 띠 행렬 💡
주대각 원소와 평행한 몇 줄의 원소들만 값을 갖고, 그 이외의 모든 원소들은 $0$인 행렬을 띠 행렬이라고 한다.
$$ \begin{pmatrix} 5 & 4 & 0 \\ 6 & 7 & 2 \\ 0 & 9 & 3 \end{pmatrix}, \begin{pmatrix} 5 & 4 & 0 & 0 \\ 0 & 7 & 2 & 0 \\ 0 & 0 & 3 & 8 \\ 0 & 0 & 0 & 9\end{pmatrix} $$
역행렬
💡 (정의) 역행렬 💡
임의의 정방 행렬 $A$에 대하여, $AB = BA = I$를 만족하는 정방 행렬 $B$가 존재할 때 $A$는 가역(역행렬이 존재함)이라고 하고, $B$는 $A$의 역행렬이라고 하며 $A^{-1}$로 표시한다.
💡 (정리) 2차 정방 행렬의 역행렬 💡
2차 정방 행렬 $A = \begin{pmatrix} a & b\\ c & d \end{pmatrix}$는 $\text{det}(A) = ad - bc \ne 0$이므로 가역이고, $A$의 역행렬은 다음과 같이 구한다.
$$ A^{-1} = \frac{1}{ad - bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix} $$
역행렬을 구하는 방법은 아주 다양합니다. 일반적으로 연립방정식을 이용하여 푸는데, 연립방정식을 푸는 방법은 가우스 소거법, 가우스-조단 방법 같이 직접적인 해를 구하는 방법과 야코비 방법, 가우스-자이델 방법 같이 반복적으로 해를 구하는 방법이 있습니다.
이에 대한 자세한 공부는 “선형대수학”에서 다루고 지금은 넘어가도록 하겠습니다.
특이 행렬
💡 (정의) 특이 행렬 💡
임의의 정방 행렬 $A$가 있을 때, $A$의 역행렬이 존재하지 않는 행렬을 특이 행렬이라고 한다. $\text{det} (A) = 0$이 되는 행렬을 말한다.
$$ \begin{pmatrix} 1 & 4 & 0 \\ 2 & 5 & 0 \\ 3 & 6 & 0 \end{pmatrix} $$
정칙 행렬
💡 (정의) 정칙 행렬 💡
임의의 정방 행렬 $A$가 있을 때, $A$의 역행렬이 존재하는 행렬을 정칙 행렬이라고 한다. $\text{det} (A) \neq 0$이 되는 행렬을 말한다.
$$ \begin{pmatrix} 1 & 3 \\ 2 & 4 \end{pmatrix} $$
직교 행렬
💡 (정의) 직교 행렬 💡
임의의 행렬 $A$에 대하여, $A^{-1} = A^{T}$가 되는 행렬을 직교 행렬이라고 한다.
부울 행렬
💡 (정의) 부울 행렬 💡
행렬의 원소들이 $0$이거나 $1$인 $m \times n$ 행렬을 부울 행렬이라고 한다.
부울 행렬의 연산과 부울 연산은 다른데, 부울 행렬에서 사용하는 연산자는 “접합”, “교합”, “부울곱”입니다.
💡 (정의) 접합 💡
$A = (a_{ij}), \ B = (b_{ij})$인 $m \times n$ 부울 행렬이 존재할 때, $A \vee B = C = (C_{ij})$를 $A$와 $B$의 접합이라고 하며, 다음과 같이 정의한다.
$$ (c_{ij}) = \begin{cases} 1, \quad a_{ij}= 1 \text{ 혹은 } b_{ij} = 1 \ 인 \ 경우 \\ 0, \quad a_{ij} \ 와 \ b_{ij} \ 가 \ 모두 \ 0 \ 인 \ 경우 \\ \end{cases} $$
💡 (정의) 교합 💡
$A = (a_{ij}), \ B = (b_{ij})$인 $m \times n$ 부울 행렬이 존재할 때, $A \wedge B = D = (d_{ij})$를 $A$와 $B$의 교합이라고 하며, 다음과 같이 정의한다.
$$ (d_{ij}) = \begin{cases} 1, \quad a_{ij} \ 와 \ b_{ij} \ 가 \ 모두 \ 1 \ 인 \ 경우 \\ 0, \quad a_{ij}= 0 \text{ 혹은 } b_{ij} = 0 \ 인 \ 경우 \end{cases} $$
💡 (정의) 부울곱 💡
$E \odot F = G = (g_{ij})$를 $E$와 $F$의 부울곱이라고 한다. 행렬 $E = (e_{ik})$가 $m \times p$ 부울 행렬이고 $F = (f_{ij})$가 $p \times n$ 부울 행렬이면 $E$와 $F$의 부울곱은 $m\times n$ 부울 행렬이 되고 다음과 같이 정의한다.
$$ (g_{ij}) = \begin{cases} 1, \quad 어떤 \ k(1 \leq k \leq p) \ 에 \ 대해 \ a_{ij}= 1,\ b_{ij} = 1 \ 인 \ 경우 \\ 0, \quad 그 \ 외에 \end{cases} $$
부울 행렬의 성질은 다음과 같습니다.
💡 (정리) 부울 행렬의 성질 💡
$A, \ B, \ C$가 부울 행렬일 때, 다음 성질이 성립한다.
- $A \vee B = B \vee A, \ A \wedge B = B \wedge A$ - (교환법칙)
- $(A \vee B ) \vee C = A \vee (B\vee C), \ (A \wedge B ) \wedge C = A \wedge (B\wedge C)$ - (결합법칙)
- $A \wedge (B\vee C) = (A \wedge B) \vee (A \wedge C), \ A \vee (B\wedge C) = (A \vee B) \wedge (A \vee C)$ - (분배법칙)
- $A \odot (B \odot C)= (A \odot B) \odot C$ - (결합법칙)
행렬식
행렬식은 기본적으로 행렬의 역행렬을 구하기 위하여 주로 사용됩니다.
💡 (정의) 행렬식 💡
행렬식은 모든 정방 행렬 $A$에 대하여 고유한 수치 값을 대응시키는 것을 말하며, $A$의 행렬식을 $\lvert A \rvert$ 또는 $\text{det}(A)$로 표시한다.
$2\times 2$인 행렬의 행렬식은 다음과 같이 정의한다.
$$ \text{det}\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} = a_{11}a_{22} - a_{12}a_{21} $$
사루스 법칙 (권장 X)
일반적인 행렬에 대한 행렬식은 사루스 법칙으로 구할 수 있습니다. 그냥 공식만 보면 이해가 어렵기에 그림을 첨부합니다.
💡 (정리) 사루스 법칙 💡
$3 \times 3$ 행렬에서 사용되는 행렬식을 구하는 공식이다. (사루스 법칙은 계산을 위한 공식으로 수학 공부 할 때는 그다지 추천하지 않는 공식입니다.)
$$ \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31} - a_{12}a_{21}a_{33} - a_{11}a_{23}a_{32} $$
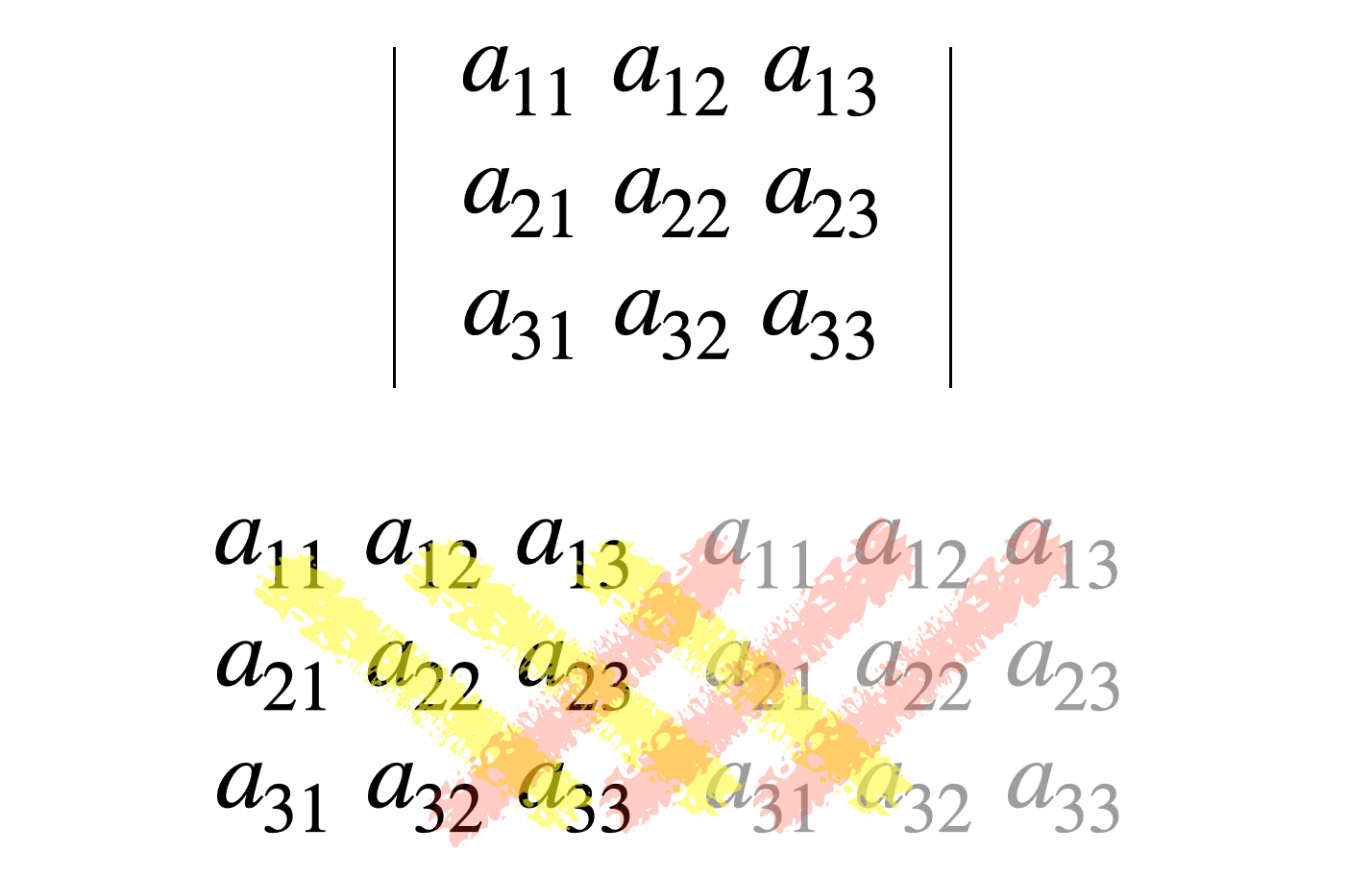
행렬식에 관한 성질
💡 (정리) 행렬식에 관한 몇 가지 성질 💡
- 행렬 $A$의 각 원소의 행과 열이 바뀌어도 $\text{det}(A)$는 변하지 않는다.
- 행렬식에서 두 개의 행이나 열을 서로 바꾸면 부호만 변한다.
- 행렬 $A$가 서로 비례하는 두 개의 행 또는 두 개의 열을 갖는 정방 행렬이면 $\text{det}(A) = 0$이다.
- 행렬식에서 특정 어느 행이나 열의 각 성분이 두 수의 합일 때, 두 개의 행렬식의 합으로 나눌 수 있다.
소행렬식과 여인수
간단한 행렬의 행렬식은 사루스 법칙으로 계산할 수 있지만, 행렬의 크기가 커지면 계산하기 쉽지 않습니다. 이러한 문제점을 해결하기 위해 행렬식을 “소행렬식”과 “여인수”를 사용하여 계산하는 방법이 고안되었습니다.
💡 (정의) 소행렬식 💡
행렬식에서 한 원소의 소행렬식은 그 원소가 있는 행과 열을 제외시킨 행렬식이다.
행렬식이 $\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix}$ 이렇게 주어진다면 $a_{11}$의 소행렬식은 $\begin{vmatrix} a_{22} & a_{23} \\ a_{32} & a_{33} \end{vmatrix}$ 이다.
💡 (정의) 여인수 💡
하나의 정방 행렬에서 한 원소의 여인수는 그 원소의 소행렬식에 부호를 붙인 값을 말한다. 즉, 행렬 $A$의 $i$번째 행과 $j$번째 열을 제거해 만든 소행렬 $A_{ij}$의 행렬식 $\begin{vmatrix} A_{ij} \end{vmatrix}$에 부호 $(-1)^{i+j}$을 붙인 값을 $A$의 $i, \ j$번째 여인수라고 한다. 부호는 다음과 같이 붙인다.
$$ \begin{vmatrix} + & - & + & \cdots \\ - &+ & - & \cdots \\ + & - & + & \cdots \\ \vdots & \vdots & \vdots \end{vmatrix} $$
💡 (정리) 여인수 전개(라플라스 전개) 💡
$M_{ij}$를 원소 $a_{ij}$의 소행렬식이라고 하면 $a_{ij}$의 여인수 $C_{ij} = (-1)^{i+ j}M_{ij}$이다. 또한, 행렬식 $\begin{vmatrix} A \end{vmatrix}$를 $n$행에 대해서 전개하면 다음과 같다.
$$ \text{det}(A) = a_{n1}\begin{vmatrix} A_{n1} \end{vmatrix} + a_{n2}\begin{vmatrix} A_{n2} \end{vmatrix} + \cdots + a_{nn}\begin{vmatrix} A_{nn} \end{vmatrix} $$
같은 방법으로 행렬식 $\begin{vmatrix} A \end{vmatrix}$를 $n$열에 대해서 전개하면 다음과 같다.
$$ \text{det}(A) = a_{1n}\begin{vmatrix} A_{1n} \end{vmatrix} + a_{2n}\begin{vmatrix} A_{2n} \end{vmatrix} + \cdots + a_{nn}\begin{vmatrix} A_{nn} \end{vmatrix} $$
참고자료 (래퍼런스)
https://www.youtube.com/watch?v=83UnOz6HiOY&list=PL127T2Zu76FuVMq1UQnZv9SG-GFIdZfLg&index=2
https://namu.wiki/w/%EB%9D%BC%ED%94%8C%EB%9D%BC%EC%8A%A4%20%EC%A0%84%EA%B0%9C
